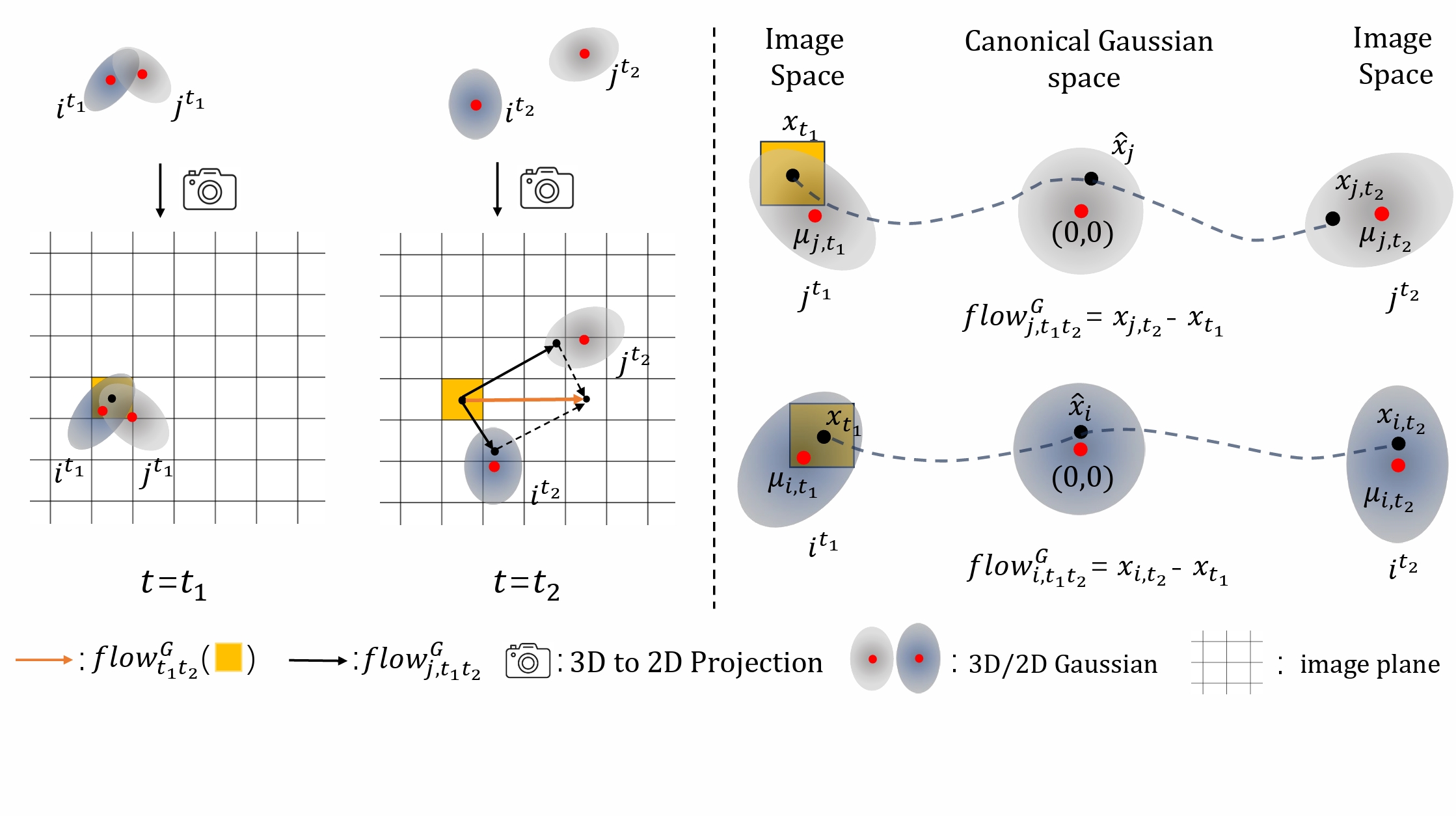
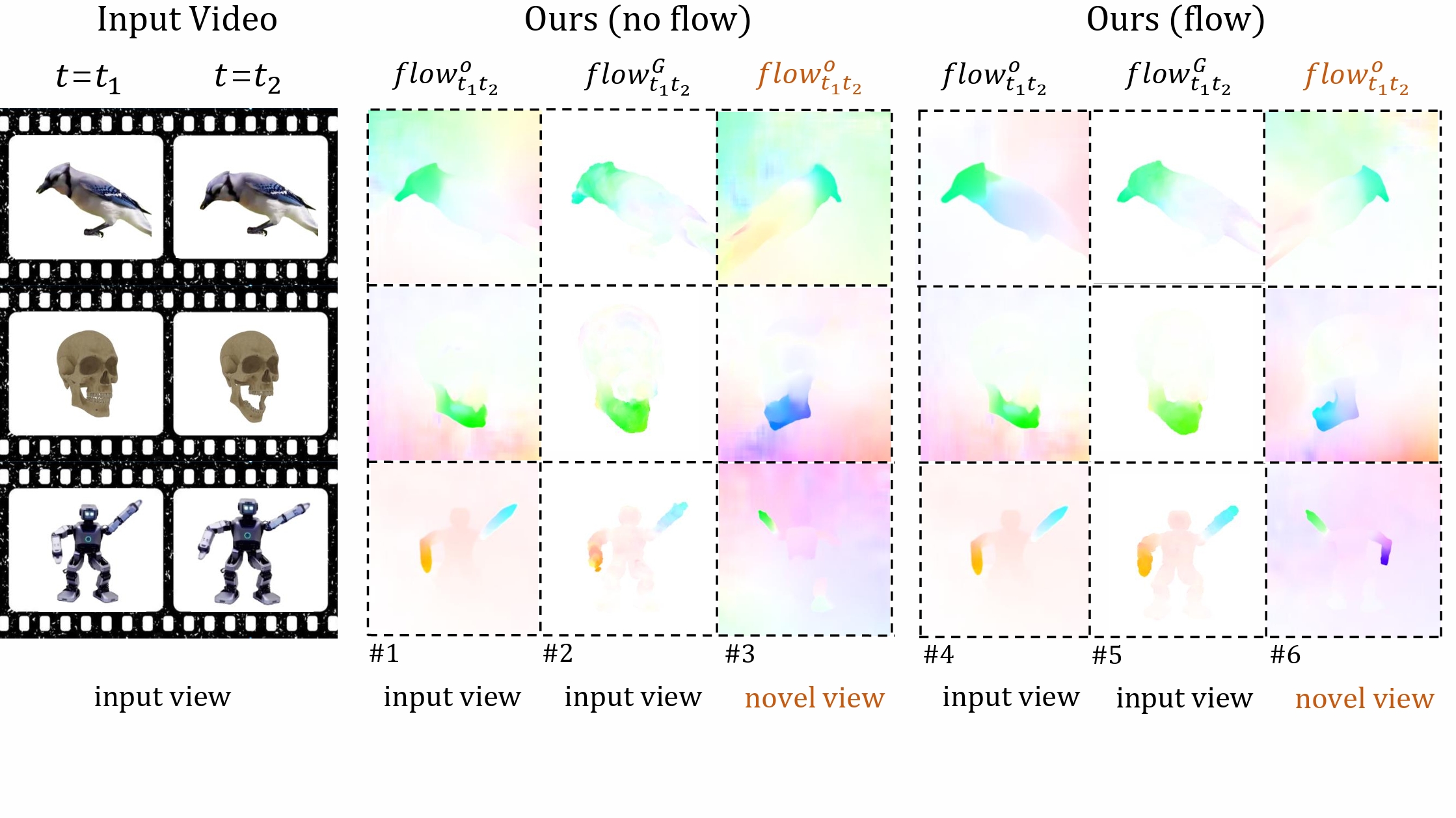
We propose Gaussian flow, a dense 2D motion flow created by splatting 3D Gaussian dynamics, which significantly benefits tasks such as 4D generation and 4D novel view synthesis. (a) Based on monocular videos generated by Lumiere and Sora, our model can generate 4D Gaussian Splatting fields that represent high-quality appearance, geometry and motions. (b) For 4D novel view synthesis, the motions in our generated 4D Gaussian fields are smooth and natural, even in highly dynamic regions where other existing methods suffer from undesirable artifacts.